Question

A triangle has legs that measure 8 cm and 10 cm. What would the length of the hypotenuse be to the nearest whole number?

Answer 1

Use the Pythagorean theorem

Explanation:

The squared length of the hypotenuse (c) is equal to the sum of the squared length of the other two sides of the right triangle (a and b) .

Therefore:

`c^(2) =a^(2) +b^(2) \\\\c=\sqrt{a^(2) +b^(2)} \\\\c=\sqrt{(8cm)^(2) +(10cm)^(2)} \\\\c=\sqrt{64 cm^(2)+100 cm^(2)} \\\\c=\sqrt{164 cm^(2)} \\\\`

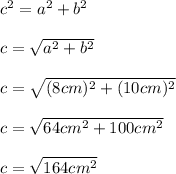
c≈12.806 cm ≈ 13 cm

The length of the hypotenuse is approximately 13 cm.

Answer 2

Answer: 13

Explanation:

The pythagorean theorem is a^2+b^2=c^2

put the two legs into the theorem

8^2+10^2=c^2

64+100=c^2

164=c^2

Now we take the square root of both sides

~12.806=c

c=13, rounded of course!

Hope this helps!