Question

What are the center and the radius of the circle who hasdiameter endpoints at (-1,1) and (14, 18)?

Answer 1

Given:

A circle has diameter endpoints at (-1, 1) and (14, 18)

The center is the mid-point of the diameter

so, we will find the midpoint using the given points as follows:

`C=((-1,1)+(14,18))/(2)=((-1+14,1+18))/(2)=((13,19))/(2)=((13)/(2),(19)/(2))`

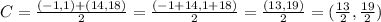
So, the coordinates of the center = C = (13/2, 19/2)

The diameter is the distance between the given points

We will find the distance using the following formula:

`d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`

Substitute with the given points

so,

`d=\sqrt[]{(14+1)^2+(18-1)^2}=\sqrt[]{15^2+17^2}=\sqrt[]{514}\approx22.67`

The radius of the circle = 0.5 * d

so, the radius = 0.5 * 22.67 = 11.335

So, the answer will be:

`\begin{gathered} center=((13)/(2),(19)/(2)) \\ radius=11.335 \end{gathered}`