Question

A block of mass m-1.4 kg is attached to a spring of spring constant k 140 N/m. The block has been extended by x = 0.12m then released from rest. The speed of the block when the elongation is x = 0.06m will be equal to:

Answer 1

Given:

Mass, m = 1.4 kg

Spring constant, k = 140 N/m

x1 = 0.12 m

Let's find the speed of the block when the elongation is x = 0.06 m

Apply the Conservation of Energy formula:

`(1)/(2)mv^2=(1)/(2)k(x^2_1-x^2_2)`

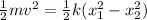
Since we are to find the speed, rewrite the formula for v:

`v=\sqrt[]{(k(x^2_1-x^2_2))/(m)}`

Where:

k = 140 N/m

x1 = 0.12 m

x2 = 0.06 m

m = 1.4 kg

Hence, we have:

`\begin{gathered} v=\sqrt[]{(140(0.12^2-0.06^2))/(1.4)} \\ \\ v=\sqrt[]{(1.512)/(1.4)} \\ \\ v=1.039\text{ m/s} \end{gathered}`

Therefore, the speed of the block when the elongation is x=0.06m is = 1.039 m/s.

ANSWER:

1.039 m/s