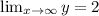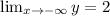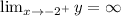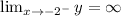Given:
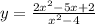
The vertical asymptotes, x= -2
The horizontal asymptotes y=2.
Aim:
We need to graph the function and find the end behavior.
Step-by-step explanation:
The graph of the function:
x-intercept is (0.5,0) and y-intercept is (0, -0.5)
End behavior:
Take the limit of the function:
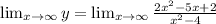
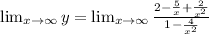
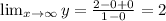
We get
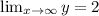
Taking the limit to negative infinity
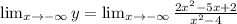
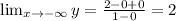
We get
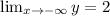
Taking the limit to -2.
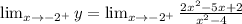
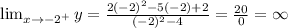
We get
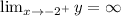
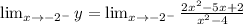
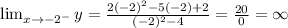
We get
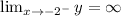
Final answer:
All limits: