Answer:
B) 12
Step-by-step explanation:
A tangent is a straight line that touches a circle at only one point.
Tangents from a common point to a circle are always equal in length.
Therefore, to find the value of x, equate the expressions for the lengths of the two tangent segments and solve for x.
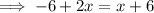

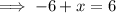

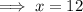
Therefore, the value of x is 12.