Question

12x³ + 7x² + 3x - 10 = 2(ax³ + x² + 2x - 5) + x(bx + c) Work out the values of a, b and c.​

Answer 1

• a = 6
• b = 5
• c = -1

Explanation:

To determine the values of a, b and c in the given equation, begin by expanding the right side:

`\begin{aligned}\implies 12x^3+7x^2+3x-10&=2(ax^3+x^2+2x-5)+x(bx+c)\\&=2ax^3+2x^2+4x-10+bx^2+cx\\&=2ax^3+2x^2+bx^2+4x+cx-10\\&=2ax^3+(2+b)x^2+(4+c)x-10\end{aligned}`

Compare the coefficients of the terms in x³ to find a:

`\begin{aligned}\implies 12x^3&=2ax^3\\12&=2a\\6&=a\end{aligned}`

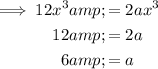
Compare the coefficients of the terms in x² to find b:

`\begin{aligned} \implies 7x^2&=(2+b)x^2\\7&=2+b\\5&=b\end{aligned}`

Compare the coefficients of the terms in x to find c:

`\begin{aligned} \implies 3x&=(4+c)x\\3&=4+c\\-1&=c\end{aligned}`

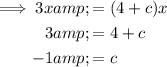
Therefore, the values of a, b and c are:

• a = 6
• b = 5
• c = -1