Question

The scale factor of triangle ABC to triangle DEF is 4:3. The area of triangle ABC is x and the area of triangle DEF is x-7. The perimeter of triangle ABC is 8+Y and the perimeter of triangle DEF is 3y-12.

a) Find the perimeter of triangle DEF
b) Find the area of triangle ABC

Answer 1

12 units and 16 units²

Explanation:

(a)

the scale factor of the perimeter is equal to the scale factor of the triangles

P of Δ ABC : P of Δ DEF = 4 : 3 ( P represents the perimeter ) , then expressing the ratios of perimeters in fractional form

`(8+y)/(3y-12)` =
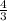`(4)/(3)` ( cross- multiply )

4(3y - 12) = 3(8 + y) ← distribute parenthesis on both sides

12y - 48 = 24 + 3y ( subtract 3y from both sides )

9y - 48 = 24 ( add 48 to both sides )

9y = 72 ( divide both sides by 9 )

y = 8

Then perimeter of Δ DEF = 3y - 12 = 3(8) - 12 = 24 - 12 = 12 units

---------------------------------------------------------------------------------

(b)

given the scale factor of triangles = 4 : 3 , then

scale factor of their areas = 4² : 3² = 16 : 9

expressing the ratios of areas of the triangles in fractional form

`(x)/(x-7)` =
`(16)/(9)` ( cross- multiply )

16(x - 7) = 9x

16x - 112 = 9x ( subtract 9x from both sides )

7x - 112 = 0 ( add 112 to both sides )

7x = 112 ( divide both sides by 7 )

x = 16

area of Δ ABC = x = 16 units²