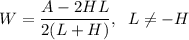Question

Please help with this question

p.s. if ur called prexicular, go away

Answer 1

`W=(A-2HL)/(2(L+H)),\;\;L\\eq -H`

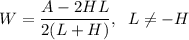
Explanation:

To make W the subject of the formula, use algebraic operations to isolate W.

Given equation:

`A=2(LW+WH+HL)`

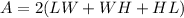
Divide both sides of the equation by 2:

`\implies (A)/(2)=(2(LW+WH+HL))/(2)`

`\implies (A)/(2)=LW+WH+HL`

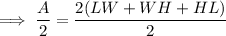
Subtract HL from both sides of the equation:

`\implies (A)/(2)-HL=LW+WH+HL-HL`

`\implies (A)/(2)-HL=LW+WH`

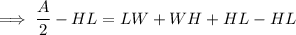
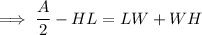
Rewrite the left side of the equation as one fraction by multiplying the term HL by 2/2:

`\implies (A)/(2)-HL \cdot (2)/(2)=LW+WH`

`\implies (A)/(2)-(2HL)/(2)=LW+WH`

`\implies (A-2HL)/(2)=LW+WH`

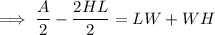
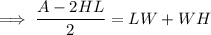
Factor out the common term W from the right side of the equation:

`\implies (A-2HL)/(2)=W(L+H)`

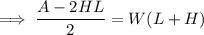
Divide both sides of the equation by (L + H):

`\implies ((A-2HL)/(2))/((L+H))=(W(L+H))/((L+H))`

`\implies W=((A-2HL)/(2))/((L+H))`

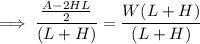
Simplify the right side of the equation:

`\implies W=(A-2HL)/(2) /(L+H)`

`\implies W=(A-2HL)/(2) \cdot (1)/((L+H))`

`\implies W=(A-2HL)/(2(L+H))`

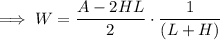
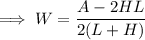
If the denominator is equal to zero, W is undefined.

Therefore, we need to impose the condition L ≠ -H.

Therefore, the final solution is:

`W=(A-2HL)/(2(L+H)),\;\;L\\eq -H`