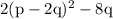Question

Factorize 2p^2 - 8(p+q)​

Answer 1

`\sf 2(p-2q)^2 - 8q`

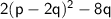
Explanation:

To factorize 2p² - 8(p+q), we can start by factoring out the greatest common factor, which is 2:

`\rm 2p^2 - 8(p+q) = 2(p^2 - 4(p+q))`

Next, we can use the difference of squares formula to factor the expression in the parentheses:

`\rm p^2 - 4(p+q) = p^2 - 4p - 4q`

`\rm = p^2 - 2(2p+2q) + 4q - 2(2q)`

`\rm = (p-2q)^2 - 4q`

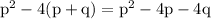
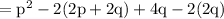
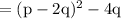
Putting this back into the original expression, we get:

`\rm 2p^2 - 8(p+q) = 2(p-2q)^2 - 8q`

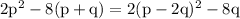
Therefore, the factorization of 2p² - 8(p+q) is:

`\rm 2(p-2q)^2 - 8q`

Answer 2

2p^2-8p-8q

Explanation:

2p^2 - 8 (p+q)

2p^2-8p-8q