The given hyperbola equation opens vertically, (Option B).
How to determine the opening of the hyperbola?
The opening of the hyperbola is determined by comparing the given equation of the hyperbola to the standard form of vertically opening and horizontally opening of hyperbola.
For horizontally open of a hyperbola, we have;
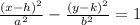
For vertically open of a hyperbola, we have;
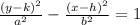
The given hyperbola is;
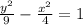
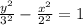
The given hyperbola equation has a positive y² coefficient, which implies that the hyperbola opens vertically.