Given:
The wavelength of the photon is,
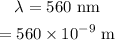
To find:
The frequency, energy, and the position of the photon on the electromagnetic spectrum
Step-by-step explanation:
We know the speed of the electromagnetic wave in a vacuum is,
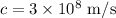
If the frequency of the photon is 'f', we can write,
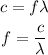
Substituting the values we get,
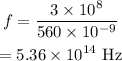
Hence, the frequency of the photon is,
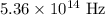
The energy of the photon is,
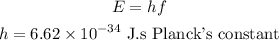
Substituting the values we get,
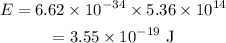
Hence, the energy of the photon is,
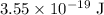
As we know the visible range is,
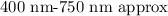
so, the given wavelength belongs to the visible range of the electromagnetic spectrum.