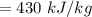Answer:
The correct answer is "430 kJ/kg". A further explanation is given below.
Step-by-step explanation:
The given values are:
T₁ = 400 k
T₂ = 800 k
The average temperature will be:
=
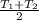
=

=
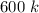
From table,
At 600 k the
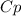 will be = 1.075
will be = 1.075
Now,
⇒ The specific enthalpy =

⇒
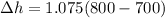
⇒