Question

A parabola with a vertex of (4, -3) passes through points (2, 5). Determine the value

of a for this parabola.
a) -1
b) 2
c) 4
d) -2

Answer 1

b) 2

Explanation:

General equation of a parabola :
`y = a(x-h)^2+k`

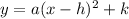
Where (h,k) is the vertex and (x,y) is a point the parabola passes through.

With the given information we can plug in these values and solve for a

First we assign variables

vertex (h,k) : (4,-3) hence h = 4 and k = -3

parabola goes through (2,5)

(x,y) = (2,5) hence x = 2 and y = 5

We then plug in these values

Equation :
`y = a(x-h)^2+k`

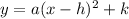
h = 4, k = -3, x = 2 and y = 5

plug in values

`5 = a(2-4)^2-3`

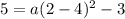
we now solve for a

5 = a(2-4)² - 3

subtract 4 from 2

5 = a(-2)^2 - 3

-2^2 = 4

5 = 4a - 3

add 3 to both sides

8 = 4a

divide both sides by 4

2 = a