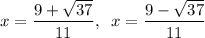Question

Solve the equation x/(x-1)+(x+2)/(x-2)+5/3=0​

Answer 1

`x=(9+√(37))/(11),\;\; x=(9-√(37))/(11)`

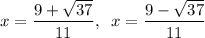
Explanation:

Given equation:

`(x)/((x-1))+((x+2))/((x-2))+(5)/(3)=0`

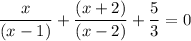
As the denominators of the fractions are different, we need to make them the same by finding the least common denominator.

The least common denominator is the product of all three denominators:

• 
  `3(x-1)(x-2)`

Rewrite the equation so that the denominators are the same:

`\implies (3x(x-2))/(3(x-1)(x-2))+(3(x-1)(x+2))/(3(x-1)(x-2))+(5(x-1)(x-2))/(3(x-1)(x-2))=0`

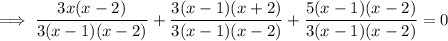
Simplify:

`\implies (3x(x-2)+3(x-1)(x+2)+5(x-1)(x-2))/(3(x-1)(x-2))=0`

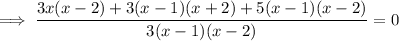
Multiply both sides by 3(x - 1)(x - 2) to eliminate the denominator:

`\implies 3x(x-2)+3(x-1)(x+2)+5(x-1)(x-2)=0`

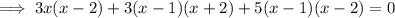
Expand:

`\implies 3x^2-6x+3(x^2+2x-x-2)+5(x^2-2x-x+2)=0`

`\implies 3x^2-6x+3(x^2+x-2)+5(x^2-3x+2)=0`

`\implies 3x^2-6x+3x^2+3x-6+5x^2-15x+10=0`

`\implies 3x^2+3x^2+5x^2+3x-6x-15x+10-6=0`

`\implies 11x^2-18x+4=0`

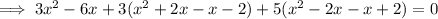
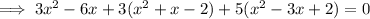
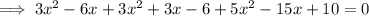
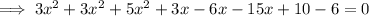
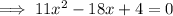
Use the quadratic formula to solve the equation.

`\boxed{\begin{minipage}{7.5 cm}\underline{Quadratic Formula}\\\\$x=(-b \pm √(b^2-4ac))/(2a)$\quad \;\;\;when $ax^2+bx+c=0$ \\\end{minipage}}`

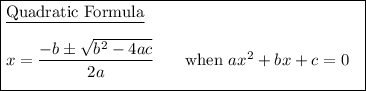
Therefore:

`a=11,\;\;b=-18,\;\;c=4`

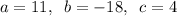
Substitute the values of a, b and c into the quadratic formula and solve for x:

`\implies x=(-(-18) \pm √((-18)^2-4(11)(4)))/(2(11))`

`\implies x=(18 \pm √(324-176))/(22)`

`\implies x=(18 \pm √(148))/(22)`

`\implies x=(18 \pm √(4 \cdot 37))/(22)`

`\implies x=(18 \pm √(4) √(37))/(22)`

`\implies x=(18 \pm 2 √(37))/(22)`

`\implies x=(9\pm √(37))/(11)`

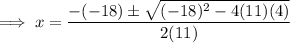
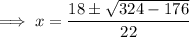
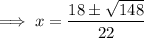
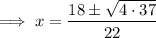
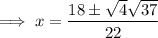
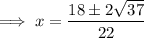
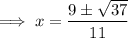
Therefore, the solutions of the equation are:

`x=(9+√(37))/(11),\;\; x=(9-√(37))/(11)`