Question

Tan-1 5/12 is equal to..

a. sin-1 12/13
b. cos-1 12/13
c.sec-1 12/13
d. cosec-1 12/13​

Answer 1

`\textsf{b)} \quad \cos^(-1)\left((12)/(13)\right)`

Explanation:

`\textsf{Let}\;\;x=\tan^(-1)\left((5)/(12)\right)`

Therefore:

`\implies \tan x=\tan\left(\tan^(-1)\left((5)/(12)\right)\right)`

`\implies \tan x=(5)/(12)`

The tan trigonometric ratio is the ratio of the side opposite the angle to the side adjacent the angle of a right triangle. Therefore, O = 5 and A = 12. Calculate the hypotenuse (H) by using Pythagoras Theorem.

`\implies a^2+b^2=c^2`

`\implies \sf O^2+A^2=H^2`

`\implies 5^2+12^2=\sf H^2`

`\implies \textsf{H}=√(5^2+12^2)`

`\implies \textsf{H}=13`

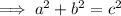
Therefore, the values are:

• θ = x
• O = 5
• A = 12
• H = 13

`\boxed{\begin{minipage}{8cm}\underline{Trigonometric ratios}\\\\$\sf \sin(\theta)=(O)/(H)\quad\cos(\theta)=(A)/(H)\quad\tan(\theta)=(O)/(A)$\\\\\\$\sf\csc(\theta)=(H)/(O)\quad\sec(\theta)=(H)/(A)\quad\cot(\theta)=(A)/(O)$\\\\where:\\\phantom{ww}$\bullet$ $\theta$ is the angle.\\\phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle.\\\phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle.\\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse.\\\end{minipage}}`

Substitute the values into the sin, cos, sec and cosec ratios then take their inverses.

`\sin x = (5)/(13)\implies \sin^(-1)(\sin x) = \sin^(-1)\left((5)/(13)\right)\implies \boxed{x= \sin^(-1)\left((5)/(13)\right)}`

`\cos x = (12)/(13)\implies \cos^(-1)(\cos x) = \cos^(-1)\left((12)/(13)\right)\implies \boxed{x= \cos^(-1)\left((12)/(13)\right)}`

`\sec x = (13)/(12)\implies \sec^(-1)(\sec x) = \sec^(-1)\left((13)/(12)\right)\implies \boxed{x= \sec^(-1)\left((13)/(12)\right)}`

`\csc x = (13)/(5)\implies \csc^(-1)(\csc x) = \csc^(-1)\left((13)/(5)\right)\implies \boxed{x= \csc^(-1)\left((13)/(5)\right)}`

Therefore, from the given answer options:

`x=\tan^(-1)\left((5)/(12)\right)=\cos^(-1)\left((12)/(13)\right)`