Question

Your answer should be a polynomial in standard form.

Answer 1

Explanation:

Using the FOIL method, we can expand this expression as follows:

(X+3)(X-5) = XX + X(-5) + 3X + 3(-5)

= X^2 - 5X + 3X - 15

= X^2 - 2X - 15

Therefore, (X+3)(X-5) = X^2 - 2X - 15.

Answer 2

Given:-

• A algebraic expression (x+3)(x-5).

To find:-

• To write it in standard form of a polynomial.

Answer:-

We need to write (x+3)(x-5) as a polynomial in standard form. As we know that the standard form of a polynomial is ,

`\implies p(x)= a_n x_n + a_(n-1)x^(n-1) + a_(n-2) x^(n-2) \dots \\`

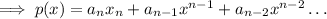
where ,

• 
  `a_n , a_(n-1) \dots` are constants.

So we can expand the given expression as ,

`\implies (x+3)(x-5)\\`

`\implies x(x-5)+3(x-5) \\`

`\implies x^2 - 5x + 3x - 15 \\`

`\implies \underline{\underline{x^2-2x-15}}\\`

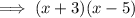
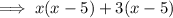
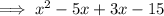
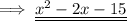
This is the polynomial in standard form.

and we are done!