Question

For the following rhombus find the measure of wy

Answer 1

Given :-

• A rhombus is given to us .
• Measure of XO is 8 and that of WO is 6 .

To find:-

• The measure of WY .

Answer:-

As we know that the diagonals of a rhombus bisects each other at right angles, so in the given figure ∆WOX is a right angled triangle, right angled at O .

Also , we know that all sides of the rhombus are equal.

So that;

`\implies WX = WY = YZ = ZX \dots (i) \\`

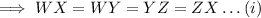
Again, in ∆WOX , by Pythagoras theorem , we have;

`\implies WX^2 = WO^2 + OX^2 \\`

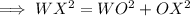
And here ,

• WO = 6
• WX = 8 .

So on substituting the respective values, we have;

`\implies WX^2 = 8^2 + 6^2 \\`

`\implies WX^2 = 64 + 36 \\`

`\implies WX^2 = 100 \\`

`\implies WX = √(100)=\boxed{10} \\`

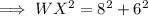
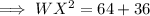
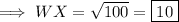
Hence the measure of WX is 10 .

Now again from equation (i) , we have;

`\implies WX = WY \\`

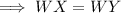
Therefore,

`\implies \underline{\underline{ WY = 10}} \\`

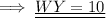
Hence the measure of WY is 10 .

and we are done!

Answer 2

WY is 5 units.

-------------------------

Properties of a rhombus:

• Diagonals bisect each-other;
• Diagonals are perpendicular to each-other.

Given diagonals of 6 and 8 units.

According to the properties we mentioned above, WY is a hypotenuse of a triangle with legs equal to the half of the diagonals.

Use Pythagorean theorem to find the length of WY:

• 
  `WY = √((6/2)^2+(8/2)^2)= √(9+16) =√(25)=5`