Answer:
The value of X is 2455.77
Step-by-step explanation:
Given the data in the question;
annual effective rate of interest of 8%, = 0.08
Now, we discount all the ash flows to present value, so we get;
3000×
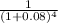 + 5000×
+ 5000×
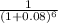 = X×
= X×
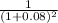 + 1000×
+ 1000×
 + 2X×
+ 2X×
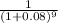
2,205.089 + 3,150.84 = 793.83 + X(
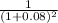 +
+
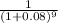 )
)
5355.929 - 793.83 = X( 0.8573 + 1.0004 )
4,562.099 = X( 1.8577 )
X = 4,562.099 / 1.8577
X = 2455.77
Therefore; value of X is 2455.77