Question

If f(x) is an exponential function where f(-3)=9 and f(7)=26, then find the value of f(2), to the nearest hundredth

Answer 1

15.30

Explanation:

You want f(2) if f(x) is an exponential function such that f(-3) = 9 and f(7) = 26.

Function

Using the given points, we can write the function as ...

`f(x)=9\left((26)/(9)\right)^{(x-(-3))/(7-(-3))}=9\left((26)/(9)\right)^{(x+3)/(10)}`

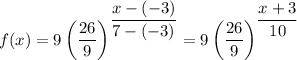
Then the value of f(2) is ...

`f(2)=9\left((26)/(9)\right)^{(2+3)/(10)}=9\sqrt{(26)/(9)}=3√(26)\approx 15.29706\\\\\boxed{f(2)\approx15.30}`

__

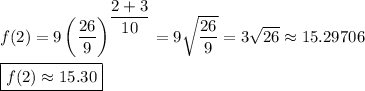
Additional comment

The form of the function is ...

f(x) = a·b^((x-x₀)/i)

where a=value at the beginning of the interval, b is the ratio of ending to beginning values, and i=interval width: x₁ -x₀. This can be written as an exponential function of e, but this is the simplest way to use given values.

Here, the "interval" is -3 to +7, and the corresponding beginning and ending values are 9 and 26, respectively.