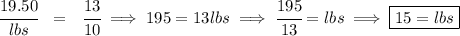Question

Will this work for it

Answer 1

to get the slope of any straight line, we simply need two points off of it, let's use those in the picture below.

`(\stackrel{x_1}{0}~,~\stackrel{y_1}{0})\qquad (\stackrel{x_2}{4}~,~\stackrel{y_2}{5.2}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{5.2}-\stackrel{y1}{0}}}{\underset{\textit{\large run}} {\underset{x_2}{4}-\underset{x_1}{0}}} \implies \cfrac{5.2}{4}\implies \cfrac{~~ ( 52)/(10 ) ~~}{4}\implies \cfrac{52}{40}\implies \cfrac{13}{10} ~~ \cfrac{\$}{lbs}`

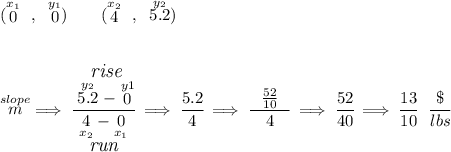
so the slope is 13/10, so we can say that the ratio of $ to lbs is 13 to 10, or $ : lbs equals 13 : 10.

now, if someone spent $19.50, what would that be in bananas?

`\cfrac{19.50}{lbs}~~ = ~~\cfrac{13}{10}\implies 195=13lbs\implies \cfrac{195}{13}=lbs\implies \boxed{15=lbs}`