Question

Write y^2+8y+16/y^2-y-20 in simplest form. State any restrictions on the variable

Answer 1

`(y+4)/(y-5)`, y≠5, y≠-4

Explanation:

Pre-Solving

We are given the fraction
`(y^2+8y+16)/(y^2-y-20)`, which we want to simplify.

Solving

We can start by factoring the quadratics that make up the fraction.

For y² + 8y + 16, we need to think about which two numbers add up to 8 and multiply to 16 (they can be the same number).

Those numbers are +4 and +4.

So, we would factor y² + 8y + 16 as (y+4)(y+4).

For y² - y - 20, we need to think about which numbers add up to -1 and multiply to -20.

Those numbers are -5 and +4.

So, y² - y - 20 would be factored as (y-5)(y+4)

Our fraction can therefore be rewritten as:

`((y+4)(y+4))/((y+4)(y-5))`

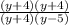
Since we have y+4 on both the numerator and denominator, we can divide both sides by y+4, leaving us with
`(y+4)/(y-5)`, which cannot be further simplified.

The question also wants us to state restrictions on the variable; remember that the denominator of a fraction cannot be zero.

For this, we need to use the original denominator; that is, we have to say (y+4)(y-5)≠0, even though we simplified the denominator earlier.

This means that:

y+4≠0

y≠-4

and

y-5≠0

y≠5

Our answer is
`(y+4)/(y-5)`, y≠5, y≠-4.