Question

A spacecraft and a staellite are at diametrically opposite position in the same circular orbit of altitude 500 km above the earth. As it passes through point A, the spacecraft fires its engine for a short interval of time to increase its speed and enter an elliptical orbit. Knowing that the spacecraft returns to A at the same time the satellite reaches A after completing one and a half orbits, determine (a) the increase in speed required, (b) the periodic time for the elliptic orbit

Answer 1

Hello the diagram related to your question is attached below

answer: a) 851 m/s

b) 8506.1 secs

Step-by-step explanation:

calculate the periodic time of the satellite using the equation below

t =
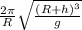`(2\pi )/(R) \sqrt{((R+h)^(3) )/(g) }` -- ( 1 )

where ; R = 6370 km

h = 500 km

g = 9.81 m/s^2

input given values into equation 1

t = 5670.75 secs

next calculate the periodic time taken by the space craft

a) determine the increase in speed

V = v -
`\sqrt{(gR^2)/(R + h) }`

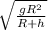
where ; v = 8463 m/s , R = 6370 km, h = 500 km

V = 851 m/s

b) Determine the periodic time for the elliptic orbit

τ =
`(3t)/(2)`

=
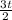
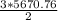`(3*5670.76)/(2)` = 8506.1 secs

attached below is the remaining part of the detailed solution