Question

Two cities are approximately 350 miles apart on the surface of the earth. Assuming that the radius of the earth is 4,000 miles, find the radian measure of the central angle with its vertex at the center of the earth that has one city on one side and another one on the other side. a. 0.0775 radians b. 0.1025 radians c. 0.0875 radians d. 0.0825 radians e. 0.1075 radians ____ 6. Name the reference angle in both degrees and radians.

Answer 1

`\mathbf{\theta = 0.0875 \ radians}`

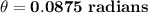
Explanation:

Given that:

The distance between city A and city B = 350 miles; &

The radius of the earth = 4000 miles

We all know that:

l = rθ

`\theta = (l)/(r)`

`\theta = (350)/(4000)`

`\mathbf{\theta = 0.0875 \ radians}`

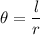
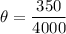
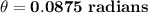
From l = rθ; recall that l = a

so;

a = rθ

350 = 4000×θ

θ = 350/4000

θ = 35/400 degree

In radians;

θ = (35/400) × (π/180)

θ = (7π /800× 180) radians