Answer:
(a) The resistor disspates 103680 joules during a 24-hour period.
(b) The heat flux of the resistor is approximately 4340.589 watts per square meter.
(c) The fraction of heat dissipated from the top and bottom surfaces is 0.045.
Step-by-step explanation:
(a) The amount of heat dissipated (
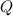 ), measured in joules, by the cylindrical resistor is the power multiplied by operation time (
), measured in joules, by the cylindrical resistor is the power multiplied by operation time (
 ), measured in hours. That is:
), measured in hours. That is:
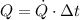 (1)
(1)
If we know that
 and
and
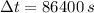 , then the amount of heat dissipated by the resistor is:
, then the amount of heat dissipated by the resistor is:

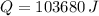
The resistor disspates 103680 joules during a 24-hour period.
(b) The heat flux (
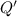 ), measured in watts per square meter, is the heat transfer rate divided by the area of the cylinder (
), measured in watts per square meter, is the heat transfer rate divided by the area of the cylinder (
 ), measured in square meters:
), measured in square meters:
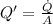 (2)
(2)
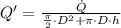 (3)
(3)
Where:
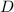 - Diameter, measured in meters.
- Diameter, measured in meters.
 - Length, measured in meters.
- Length, measured in meters.
If we know that
 ,
,
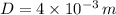 and
and
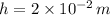 , the heat flux of the resistor is:
, the heat flux of the resistor is:
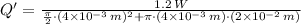
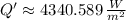
The heat flux of the resistor is approximately 4340.589 watts per square meter.
(c) Since heat is uniformly transfered, then the fraction of heat dissipated from the top and bottom surfaces (
 ), no unit, is the ratio of the top and bottom surfaces to total surface:
), no unit, is the ratio of the top and bottom surfaces to total surface:
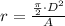 (3)
(3)
If we know that
 and
and
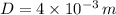 , then the fraction is:
, then the fraction is:
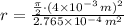
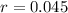
The fraction of heat dissipated from the top and bottom surfaces is 0.045.