The probability that the experiment results in fewer than 2 successes is 0.555 to three decimal places.
Solving probability involving binomial expression.
The probability mass function for a binomial expression can be expressed as:
 .
.
Here;
- n = no. of trials = 9
- k = no. of success
- p = probability of success = 0.16
- (1 - p) = probability of failure
Now, to find the probability that the experiment results is fewer than 2 successes, we have
P(X < 2) = P(X = 0) + P(X = 1)

Solving each term, we have:
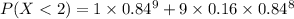
P(X < 2) = 0.2205 + 0.3343
P(X < 2) = 0.5548
Thus, the probability that the experiment results in fewer than 2 successes is 0.555 to three decimal places.