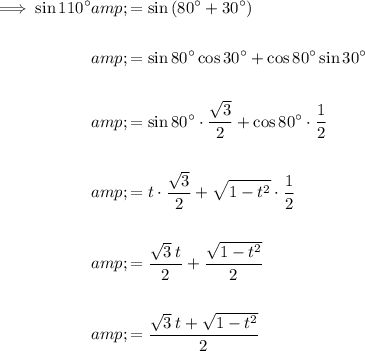Question

Question 4 trigonometry

Answer 1

See below for proof.

Explanation:

Rewrite 110° as the sum of 80° and 30°:

`\implies \sin 110^(\circ)=\sin \left(80^(\circ)+30^(\circ)\right)`

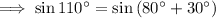
Given sin 80° = t and using the trigonometric identity sin²θ + cos²θ = 1, find an expression for cos 80° in terms of t:

`\implies \sin^280^(\circ)+\cos^280^(\circ) =1`

`\implies t^2+\cos^280^(\circ) =1`

`\implies \cos^280^(\circ) =1-t^2`

`\implies \cos80^(\circ) =√(1-t^2)`

`\boxed{\begin{minipage}{6.5 cm}\underline{Sine Double Angle Identity}\\\\$\sin (A \pm B)=\sin A \cos B \pm \cos A \sin B$\\\end{minipage}}`

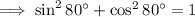
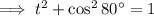
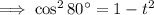
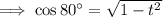
Apply the Sine Double Angle identity to sin (80° + 30°):

`\implies \sin \left(80^(\circ)+30^(\circ)\right)=\sin 80^(\circ) \cos 30^(\circ) + \cos 80^(\circ) \sin 30^(\circ)`

`\textsf{As}\;\; \boxed{\cos 30^(\circ)=(√(3))/(2)}\;\;\textsf{and}\;\;\boxed{\sin30^(\circ)=(1)/(2)}\:,\; \textsf{substitute these values into the equation:}`

`\implies \sin \left(80^(\circ)+30^(\circ)\right)=\sin 80^(\circ)\cdot (√(3))/(2) + \cos 80^(\circ) \cdot (1)/(2)`

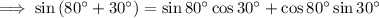
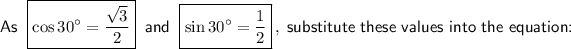
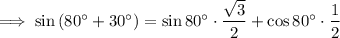
Substitute the expressions for sin 80° and cos 80° in terms of t:

`\implies \sin \left(80^(\circ)+30^(\circ)\right)=t\cdot (√(3))/(2) +√(1-t^2) \cdot (1)/(2)`

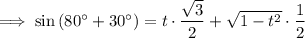
Simplify:

`\implies \sin \left(80^(\circ)+30^(\circ)\right)=(√(3)\:t)/(2) +(√(1-t^2) )/(2)`

`\implies \sin \left(80^(\circ)+30^(\circ)\right)=(√(3)\:t+√(1-t^2))/(2)`

`\textsf{Thus proving:}\;\;\;\sin \left(110^(\circ)\right)=(√(3)\:t+√(1-t^2))/(2)`

-------------------------------------------------------------------------------------------

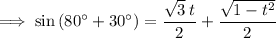
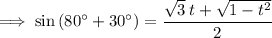
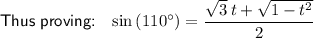
As one calculation:

`\begin{aligned}\implies \sin 110^(\circ)&=\sin \left(80^(\circ)+30^(\circ)\right)\\\\&=\sin 80^(\circ) \cos 30^(\circ) + \cos 80^(\circ) \sin 30^(\circ)\\\\&=\sin 80^(\circ)\cdot (√(3))/(2) + \cos 80^(\circ) \cdot (1)/(2)\\\\&=t\cdot (√(3))/(2) +√(1-t^2) \cdot (1)/(2)\\\\&=(√(3)\:t)/(2) +(√(1-t^2) )/(2)\\\\&=(√(3)\:t+√(1-t^2))/(2)\end{aligned}`