Question

A 30-foot ladder leans against a wall so that the base of the ladder is 8 feet from the base of the building. What angle does the ladder make with the ground?

Answer 1

INFORMATION:

We know that:

- A 30-foot ladder leans against a wall

- the base of the ladder is 8 feet from the base of the building

And we must find the angle between the ladder and the ground

STEP BY STEP EXPLANATION:

To solve the problem properly, we can make a sketch of the situation

Since we must find an angle from a right triangle, we can use a trigonometric function

We know the values of the hypotenuse and the adjacent side to the angle

The hypotenuse is the ladder and the adjacent side is the distance between the base of the ladder and the base of the building. So, hypotenuse = 30 and adjacent = 8

We can use the trigonometric function Cosθ

`\begin{gathered} cos\theta=(adjacent)/(hypotenuse) \\ \text{ Replacing their values,} \\ cos\theta=(8)/(30) \end{gathered}`

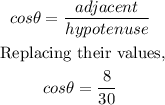
Finally, we must solve for θ

`\begin{gathered} \theta=cos^(-1)((8)/(30)) \\ \theta=74.5340\degree \end{gathered}`

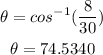
ANSWER:

The angle between the ladder and the ground is 74.5340°