Question

Suppose an exponential function in the form of g(x)=a(b)^x+c +d is used to find the equation for g^-1 (x). What would the argument of the logarithmic function be? (The "argument" is the part of the logarithm that is inside the parenthesis). What role does the argument of the function play in the graph of the function?​

Answer 1

Explanation:

`g(x) = ab {}^((x + c)) + d`

Let solve for the variable x.

`y = ab {}^(x + c) + d`

`y - d = ab {}^(x + c)`

`(y - d)/(a) = b {}^(x + c)`

`log_(b)( (y - d)/(a) ) = x + c`

`log_(b)( (y - d)/(a) ) - c = x`

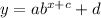
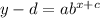
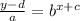
Swap x and y, Replace y with g inverse.

`log_(b) ( (x - d)/(a) ) - c = g {}^( - 1) (x)`

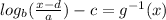
The argument inside the logarithm will be

`(x - d)/(a)`

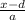
The argument will first cause a horizontal shift d units to the left or right to the graph, then the graph would then cause a horizontal stretch by some factor a