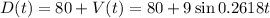Question

Outside temperature over a day can be modeled as a sinusoidal function. Suppose you know the temperature is 80 degrees at midnight and the high and low temperature during the day are 89 and 71 degrees, respectively. Assuming t is the number of hours since midnight, find an equation for the temperature, D, in terms of t.

Answer 1

The equation is given by:

`D(t) = 80 + 9sin(0.2618t)`

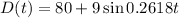
Explanation:

Sine function:

Has the following format:

`y = Asin(bx)`

In which A is the amplitude and
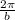`(2\pi)/(b)` is the period.

Suppose you know the temperature is 80 degrees at midnight and the high and low temperature during the day are 89 and 71 degrees

This means that the amplitude of the sinusoidal variation function is 89 - 80 = 80 - 71 = 9. This means that
`A = 9`

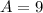
During a 24-hour day, which means that the period is 24. So

`(2\pi)/(b) = 24`

`24b = 2\pi`

`b = (2\pi)/(24)`

`b = 0.2618`

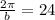
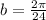
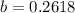
So the variation is:

`V(t) = 9sin(0.2618t)`

Assuming t is the number of hours since midnight, find an equation for the temperature, D, in terms of t.

Initial temperature of 80, so:

`D(t) = 80 + V(t) = 80 + 9sin(0.2618t)`