Question

A car manufacturer produced 5.000 cars for a limited edition model Dealers sold all of these cars at mean price of $36,000 with a standard deviation of $3,000. Suppose we were to take random samples of 9 of these cars and calculate the sample mean price for each sample. Calculate the mean and standard deviation of the sampling distribution of .

Answer 1

Answer: Mean = $36,000 and standard deviation = $1000.

Explanation:

The mean and the standard deviation of the sampling distribution of the sample mean:

`Mean=\mu\\\\Standard\ deviation = (\sigma)/(√(n))` , where n =sample size.

Here, we are given

`\mu=\$36000,\ \ \sigma=\$3,000`

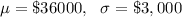
n= 9

Then, the mean and the standard deviation of the sampling distribution of the sample mean:

`Mean=\$36000,\ \ Standard\ deviation=(3000)/(√(9))=(3000)/(3)=\$1000`

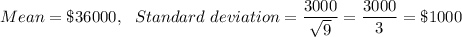
Hence, Mean = $36,000 and standard deviation = $1000.