Question

The second term in a geometric sequence is 20. The fourth term in the same

sequence is 45/4, or 11.25. What is the common ratio in this sequence?
Answer here
SUBMIT

Answer 1

0.75

Explanation:

Geometric sequence:

`a_(n) = a_(1) r^(n-1)`

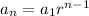
Where:

`a_(n)` =
`n^(th)` term

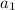`a_(1)` = First term

r = common ratio

We are provided with the second and fourth terms:

`a_(2) = a_(1) r^(2-1)`
=
`20 = a_(1)r`

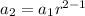
Formulate an expression of
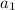`a_(1)` in terms of r:

∴
`a_(1) = (20)/(r)` ——- (equation i)

`a_(4) = a_(1) r^(4-1)`

=
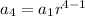
`11.25 = a_(1) r^(3)` ——- (equation ii)

Substitute (equation i) into (equation ii) and solve for r:

`11.25 = ((20)/(r))(r^(3))`

`11.25 = (20)(r^(3-1))`

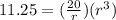
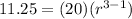
Isolate the r term by making it the subject of the equation:

`11.25 = 20r^(2)`

`r^(2) = (11.25)/(20)`

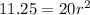
Taking the square root on both sides to get rid of the square:

`r = \sqrt{(11.25)/(20)}`

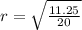
∴r = Common ratio = 0.75