Question

A ball bearing is placed on an inclined plane and begins to roll. The angle of elevation of the plane is . The distance (in meters) the ball bearing rolls in t seconds is s(t) = 4.9(sin )t2.

Answer 1

The speed of the ball bearing is given by the first derivative of the distance function.

Using the power rule in our function, we have

`\begin{gathered} s^(\prime)(t)=(d)/(dt)(4.9(\sin \theta)t^2)=4.9(\sin \theta)(d)/(dt)(t^2)=4.9(\sin \theta)(2t) \\ s^(\prime)(t)=9.8(\sin \theta)t \end{gathered}`

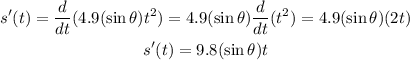
To complete the table we just have to evaluate the sine function on the given θ values.

`\begin{gathered} \theta=0\Rightarrow s^(\prime)(t)=9.8(\sin 0)t=9.8\cdot0\cdot t=0 \\ \theta=(\pi)/(4)\Rightarrow s^(\prime)(t)=9.8(\sin ((\pi)/(4)))t=9.8\cdot\frac{\sqrt[]{2}}{2}\cdot t=4.9\sqrt[]{2}t \\ \theta=(\pi)/(3)\Rightarrow s^(\prime)(t)=9.8(\sin ((\pi)/(3)))t=9.8\cdot\frac{\sqrt[]{3}}{2}\cdot t=4.9\sqrt[]{3}t \\ \theta=(\pi)/(2)\Rightarrow s^(\prime)(t)=9.8(\sin ((\pi)/(2)))t=9.8\cdot1\cdot t=9.8t \\ \theta=(2\pi)/(3)\Rightarrow s^(\prime)(t)=9.8(\sin ((2\pi)/(3)))t=9.8\cdot\frac{\sqrt[]{3}}{2}\cdot t=4.9\sqrt[]{3}t \\ \theta=(3\pi)/(4)\Rightarrow s^(\prime)(t)=9.8(\sin ((3\pi)/(4)))t=9.8\cdot\frac{\sqrt[]{2}}{2}\cdot t=4.9\sqrt[]{2}t \\ \theta=\pi\Rightarrow s^(\prime)(t)=9.8(\sin \pi)t=9.8\cdot0\cdot t=0 \end{gathered}`

According to the table, the biggest value for the speed happens at θ = π/2.