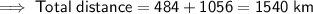Question

David's airplane trip took 2.2 hours. For one-fourth of that time, the airplane flew at a speed of 880 km/h, and for the rest of the time, it flew at a speed of 640 km/h. What distance did david travel?

Answer 1

For half of that time, the airplane flew at a speed of 900 km/h, and for the rest of the time, it flew at a speed of 760 km/h.

Explanation:

Answer 2

The distance David travelled was 1540 km.

Explanation:

To find the total distance David travelled, calculate the distance of the two legs of the journey separately, then add them together.

First leg of the journey

David flew at a speed of 880 km/h for one-fourth of 2.2 hours.

One-fourth of 2.2 hours is:

`\implies \sf (1)/(4) \cdot 2.2 = 0.55\;\sf hours`

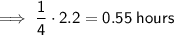
To calculate the distance of this leg of the journey, substitute the given speed and found time into the Speed Distance Time formula.

`\implies \sf Speed=(Distance)/(Time)`

`\implies \sf 880\;km/h=(Distance)/(0.55\;h)`

`\implies \sf Distance=880\;km/h \cdot 0.55\;h`

`\implies \sf Distance=484\;km`

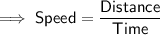
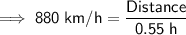
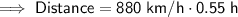
Therefore, David travelled a distance of 484 km during the first leg of his journey.

Second leg of the journey

David flew at a speed of 640 km/h for the remainder of the journey.

The length of time of the second leg of the journey is 2.2 hours less 0.55 hours:

`\implies \sf 2.2-0.55=1.65\;hours`

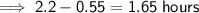
To calculate the distance of this leg of the journey, substitute the given speed and found time into the Speed Distance Time formula.

`\implies \sf Speed=(Distance)/(Time)`

`\implies \sf 640\;km/h=(Distance)/(1.65\;h)`

`\implies \sf Distance=640\;km/h \cdot 1.65\;h`

`\implies \sf Distance=1056\;km`

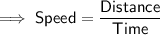
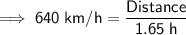
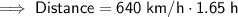
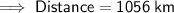
Therefore, David travelled a distance of 1056 km during the second leg of his journey.

Total distance

Therefore, the total distance is the sum of the distances of the two legs of the journey:

`\sf \implies Total\;distance=484+1056=1540\;km`