Question

100 points G.GPE.4 ■ Use coordinates to prove simple geometric theorems algebraically;

for example prove or disprove that the point (1, √3) lies on the circle centered at
the origin and containing the point (0, 2).

Answer 1

Given:-

• A circle is centred at origin .
• It contains a point (0,2) .

To prove/disprove :-

• The point (1,√3) lies on the circle.

Answer :-

Here we are given that the circle is centred at origin that is at (0,0) . And it contains a point (0,2) . Using distance formula we can find the radius of the circle. The distance formula is ,

`\implies d =√((x_2-x_1)^2+(y_2-y_1)^2)\dots (i)\\`

and here,

• 
  `d = r`
• 
  `x_1 = 0`
• 
  `x_2 = 0`
• 
  `y_1 = 0`
• 
  `y_2 = 2`

on substituting the respective values, in (i) , we have;

`\implies r = √( (0-0)^2 + (2-0)^2) \\`

`\implies r =√( 2^2) \\`

`\implies r = 2 \ units \\`

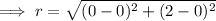
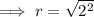
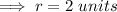
hence the radius of the circle is 2 units .

Now find the distance of the point (1,√3) from the centre using distance formula and if
`d = r`then the point lies on the circle.

`\implies d =√( (1-0)^2+(\sqrt3-0)^2)\\`

`\implies d = √( 1 + 3 ) =√(4) \\`

`\implies \underline{\underline{ d = 2 \ units}} \\`

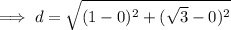
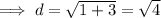
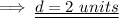
Hence here ,

`\implies d = r \\`

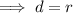
So the given point lies on the circle.

and we are done!