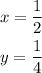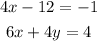
We want to solve this system using a matrix.
The first step is write a matrix whose each line will correspond to a equation and each term will correspond to a coeficient. The terms of the firs colum will correspond to the coeficients of x, the terms of the second colum will correspond to the coeficients of y and the terms of the third colum will correspond to the independent term in the right side of the equation:
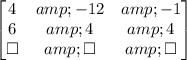
Now, we must conduct operations to escalonate the terms corresponding to the coefficients multiplying x and y
First, we multiply the second line by 3:
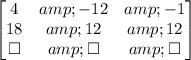
Then, we add line 2 to line 1:
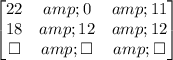
Now, we divide line 1 by 22
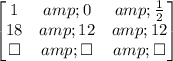
Then, we subtract 18 times line 1 from line 2:

Now, we divide line 2 by 12:
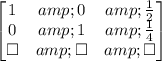
Finally, we can rewrite these terms in the form of equations and obtain the solution: