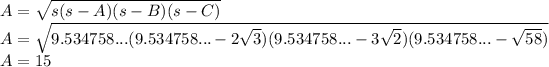Question

What is the area, in square units, of triangle DEF?

Triangle DEF, with vertices D(3,-9), E(9,-5), and F(6,-2), is drawn on the coordinate grid below.

Answer 1

15 square units

Explanation:

i am using Heron's formula for this question

Firstly, lets calculate the lengths of the triangle. We can do this by using the formula:

`length=\sqrt{(y_(2)\\-y_(1)\\)^(2)+(x_(2)\\-x_(1)\\)^(2) }`

Calculating the length between D (3,-9) and E (9,-5):

`length(A)=\sqrt{(-9-(-5))^(2)+(3-9)^(2) } \\length(A)=2√(13)`

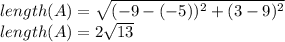
Calculating the length between F (6,-2) and E (9,-5):

`length(B)=\sqrt{(-2-(-5))^(2)+(6-9)^(2) }\\length(B)=3√(2)`

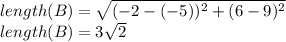
Calculating the length between D (3,-9) and F (6,-2):

`length(C)=\sqrt{(-9-(-2))^(2)+(3-6)^(2) }\\length(C)=√(58)`

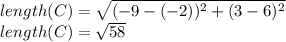
Now, we can find the semi-perimeter with the formula:

`s=(A+B+C)/(2)`

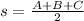
where A, B and C are the lengths

The semi-perimeter is:

`s=(2√(13)+3√(2)+√(58) )/(2)\\s=9.534758... (store \, the \, full \, value \, in \, your \, calculator)`

The formula for the area of the triangle:

`A=√(s(s-A)(s-B)(s-C))\\A=\sqrt{9.534758...(9.534758...-2√(3))(9.534758...-3√(2))(9.534758...-√(58) ) }\\A=15`

Answer 2

Below

Explanation:

You COULD calculate the lengths of the three sides and then use Heron's Formula to calculate the area.....

Here is perhaps an easier way (see image)

calculate the entire area of the rectangle then subtract the 3 smaller RIGHT triangles from the total

Area of rectangle = 6 x 7 = 42 units^2

triangles 1/2 ( 3 x 7 + 3 x 3 + 4 x 6 ) = 27 units^2

42 - 27 = 15 units^2 = area of given triangle