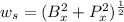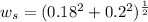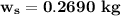Question

In a cheese factory, 4.5-kg blocks of cheese are cut manually. For a large number of blocks, the standard deviation of the cutting process is measured and found to be 0.10 kg. The measurement was done with a scale with an accuracy of 1.5% of the full scale of 12 kg. Calculate the total uncertainty of the weight of the blocks of cheese at a 95 % confidence level.

Answer 1

0.2690 kg

Explanation:

Given that:

For cutting a 4.5 kg block of cheese; the standard deviation:

`S_x = 0.1 \ kg`

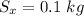
For a large no of blocks, at 95% confidence level;

Using the t table; where the degree of freedom is infinity or > 30

t-distribution (t) = 2

∴

`P_x = tS_x`

`P_x = 2 * 0.1`

`P_x = 0.2 \ kg`

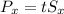
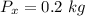
The system uncertainty as a result of the accuracy
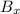`B_x` is:

`B_x = 1.5\% \ of \ reading`

`B_x = ((1.5)/(100))(12 kg)`

`B_x = 0.18 \ kg`

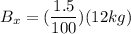
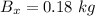
The total uncertainty for a single experiment with a 95% confidence interval will be:

`w_s = ( B_x^2 + P_x^2)^{(1)/(2)`

`w_s = (0.18^2 + 0.2^2)^{(1)/(2)`

`\mathbf{w_s = 0.2690 \ kg}`