Given:
Mean= 98
Standard Deviation= 3
Sample = 42
Observed value = 98.6
To determine the probability that the sample mean will be greater than 98.6 gallons, we first note the z-score formula:

Next, we plug in what we know:
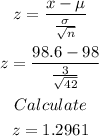
Then, we also note that:
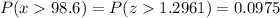
Therefore, the probability that the sample mean will be greater than 98.6 gallons is: 0.0975