Question

Answer the following questions. will give alot of points 1.The angle of depression from an airplane to the top of an air traffic control tower is 56°. If the tower is 320 feet tall and the the airplane is flying at an altitude of 7,450 feet, how far away is the airplane from the control tower? Round to the nearest tenth.

2.the town park does an outdoor movie night every Saturday during the summer on a large screen. Kate is sitting 36 feet from the base of the screen, watching a movie with her family. If the angle of elevation from Kate to the top of the screen is 24°, how tall is the movie screen? Round to the nearest tenth.

Answer 1

Question 1

How far away is the airplane from the control tower?

`\boxed{4809.2 \;feet}`

Question 2
Height of the movie screen =
`\h = \boxed{16\;\text{feet }}`

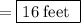
Explanation:

In both questions, a diagram of the scenario makes everything easier to understand

Question 1

Look at the first image as a reference to the explanation for this question.

BF represents the horizontal distance, d, of the plane from the control tower

The angle of depression 56° is the measure of ∠CDE

Since lines CD and BF are parallel to each other - both being horizontal lines - m ∠DBF = 56° (alternate interior angles)

The vertical height of the plane relative to the top of the control tower
= height of plane above ground - height of control tower
= 7450 - 320

= 7130 feet

The triangle BDF is a right triangle where the legs are 7130 feet and d feet

The equation relating the two legs of a right triangle and the angle formed is

`\tan\theta = \frac{\text{Side Opposite}}{\text{Side Adjacent}}}`

Here we have

`\theta = 56^\circ,\\\\\text{Side opposite } = 7130\\\\\text{Side adjacent} - d`

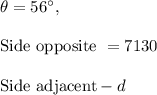
Plugging these into the equation for
`\tan\theta` we get

`\tan 56^\circ = (7130)/(d)`

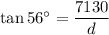
Cross multiplying we get

`d = (7130)/(\tan\; 56^\circ)\\\\= (7130)/(1.48256)\\\\= 4,809. 2 feet`

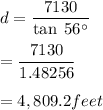
Question 2

The strategy for solution is almost the same. Instead of angle of depression we are looking at the angle of elevation. And. instead of computing the horizontal distance we are asked to compute the height

The relevant diagram is attached

Using the same formula as for Question 1

`\tan\;24^\circ = (h)/(36)\\\\(h)/(36) = \tan\;24^\circ\\\\h = \tan\;24^\circ * 36\\\\h = 0.4452 * 36\\\\h = 16.0 \;\text{feet rounded to the nearest tenth}`