Question

Find an equation for the perpendicular bisector of the line segment whose endpoints are (-3,9) and (9,5).

Answer 1

to find a perpendicular line to another we need to know the slope of the first line, Fortunately we can find the slope with the two points

`m=(y2-y1)/(x2-x1)`

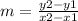
where m is the slope (x2,y2) a point right from (x1,y1)

on this case (x2,y2)=(9,5) and (x1,y1)=(-3,9)

so replacing

`\begin{gathered} m=(5-9)/(9-(-3)) \\ m=-(1)/(3) \end{gathered}`

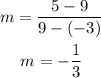
knowing the slope we can find the slope of the perpendicular and this is all than we need to make to lines paralels:

reverse slope and change the sign

so the slope of the new line is 3

`-(1)/(3)\longrightarrow3`

to write a equation we can use the general form

`y=mx+b`

where y is the solution, m the slope and x the variable and b it doesnt matter on this case because two lines are only made perpendicular by their slope, so you can use any number

like this

`y=3x+1`

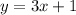
that was the equation