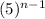Question

2, 10, 50, 250, 1250

Write the explicit form of the sequence above.

Answer 1

Answer:
`a_(n)=2` ×
`(5)^(n-1)`

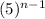
The explicit formula for the given sequence is
`a_{n` = 2 x
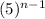`(5)^(n-1)`and this can be determined by using the formula of the nth term of the geometric progression.

Given :

Sequence --- 2, 10, 50, 250, 1250, …

The following steps can be used in order to determine the explicit formula for the given sequence:

Step 1 - Write the given sequence.

2, 10, 50, 250, 1250, …

Step 2 - The given sequence is in geometric progression.

Step 3 - The geometric ratio is calculated as:

r = 10/2 = 5

Step 4 - The nth term formula in the geometric progression is given below:

`a_(n) = ar^(n-1)`

where 'a' is the first term and 'r' is the geometric ratio.

Step 5 - Now, substitute the values of the known terms in the above formula.

`a_(n) = 2` ×
`(5)^(n-1)`