Question

How do I solve this and what’s the answers

Answer 1

A.

`(12)/(5)`

Explanation:

tan ? =
`(front)/(side)`

In picture, we know tan F = tan R

the length of side;

= √oblique² - front²

= √13² - 12²

= √169 - 144

= √25

side = 5 cm

So, tan R =
`(front)/(side)`

=
`(12)/(5)`

So, the answer is A

Answer 2

Given :-

• Two right angled triangles which are similar.

To find:-

• The value of tan R .

Answer:-

Since here the given two triangles are similar, therefore,

• 
  `\angle DFE =\angle CRA`
• the ratio of corresponding two sides of one triangle will be equal to the ratio of corresponding two sides of second triangle.

Hence ,

`\implies (DE)/(DF)=(CA)/(AR)\\`

`\implies \tan F = \tan R \dots (1) \\`

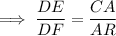
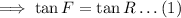
Now in ∆DEF ,

• DF = 13ft
• EF = 12ft
• DE = ?

So on using Pythagoras theorem we have,

`\implies DE^2 + EF^2 = DF^2 \\`

`\implies DE^2 = (13ft)^2-(12ft)^2\\`

`\implies DE^2 = 169ft^2-144ft^2\\`

`\implies DE^2 = 25ft^2 \\`

`\implies DE =√(25 ft^2) \\`

`\implies \underline{\underline{ DE = 5\ ft.}} \\`

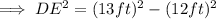
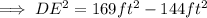
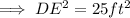
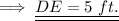
Now again we know that ,

`\implies \tan\theta =(perpendicular)/(base)\\`

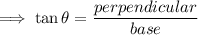
And here ,

`\implies \theta = \angle F \\`

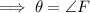
So ,

`\implies \tan F = (DE)/(EF) \\`

`\implies \tan F =(5ft)/(12ft)=\boxed{(5)/(12)} \\`

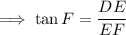
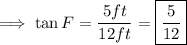
Hence from equation (1) , we have;

`\implies \underline{\underline{\tan R =(5)/(12)}} \\`

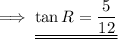
and we are done!