Given:
Cost of each DVD = $x
Number of DVDs sold = 200 - 8x
Let's solve for the following:
A) The store sold 80 DVDs yesterday. What was the price of each DVD?
To find the price of each DVD if 80 DVDs were sold, we have the equation:
200 - 8x = 80
Let's solve for x.
Subtract 200 from both sides:
200 - 200 - 8x = 80 - 200
-8x = -120
Divide both sides by -8:

Therefore, the price of each DVD was $15
B) The store wants to sell at least 80 DVDs. What range of prices will ensure this.
To find the range of prices, we have the inequality:
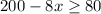
Let's solve for x.
Subtract 200 from both sides:
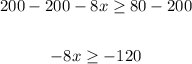
Divide both sides by -8:
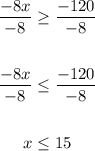
The range of prices that will ensure this must be from $0 to $15
This means the price of each DVD must not be more than $15
C) The store wants to sell at least