Answer:
Answer is explained below in the explanation section.
Step-by-step explanation:
Solution:
An investor has up to $250,000 to invest in three types of investment.
Type A pays 8% annually and has risk factor of 0.
Type B pays 10% annually and has risk factor of 0.06.
Type C pays 14% annually and has risk factor of 0.10.
So,
Decision Variables are:
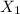 = Total Amount invested in Type A.
= Total Amount invested in Type A.
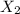 = Total Amount invested in Type B.
= Total Amount invested in Type B.
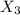 = Total Amount invested in Type C.
= Total Amount invested in Type C.
So, the Objective Function will be:
Objective function:
Max Z = 0.08
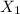 + 0.10
+ 0.10
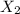 + 0.14
+ 0.14
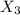
And the Constraints will be:
1. Total Amount Variable:
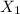 +
+
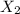 +
+
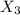
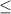 250000
250000
2. Total Risk is no greater than 0.05:
0
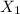 + 0.06
+ 0.06
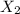 + 0.10
+ 0.10
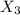
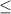 0.05
0.05
3. At least one fourth of the total amount invested to be allocated to Type A investment.
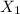
 0.25 (
0.25 (
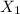 +
+
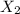 +
+
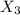 )
)
0.75
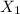 - 0.25
- 0.25
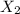 - 0.25
- 0.25
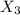
 0
0
4. At least one fourth of the total amount to be allocated to Type B investment.
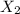
 0.25 (
0.25 (
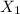 +
+
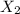 +
+
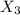 )
)
-0.25
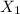 + 0.75
+ 0.75
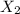 - 0.25
- 0.25
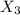
 0
0
5. And the non- negativity constraints are:
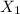 ,
,
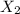 , and
, and
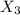
 0
0