Let C be the number of chidren and A be the number of adults. Then, we have
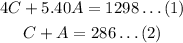
Then, we have 2 equations in 2 unknonws.
Solving by elimination method
If we multiply equation (2) by -4, we get an equivalent system of equation:
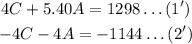
By adding both equations, we have
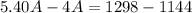
because 4C - 4C =0. This last expression gives
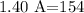
By moving the coefficient of A to the right hand side, we get
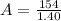
and A is equal to 100, that is A=110.
Now, we can substitute this result into equation (2). It yields
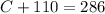
By moving +110 to the right hand side, we have
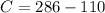
then, C is equal to 176.
Therefore, there are 176 children and 110 adults.