Question

The admission feet at park is $4.00 for children and $5.40 for adults. On a certain day, 286 people entered the park, and the admission fees collected totaled 1298 dollars. How many children and how many adults were admitted? number of children equalsnumber of adults equals

Answer 1

Let C be the number of chidren and A be the number of adults. Then, we have

`\begin{gathered} 4C+5.40A=1298\ldots(1) \\ C+A=286\ldots(2) \end{gathered}`

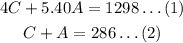
Then, we have 2 equations in 2 unknonws.

Solving by elimination method

If we multiply equation (2) by -4, we get an equivalent system of equation:

`\begin{gathered} 4C+5.40A=1298\ldots(1^(\prime)) \\ -4C-4A=-1144\ldots(2^(\prime)) \end{gathered}`

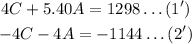
By adding both equations, we have

`5.40A-4A=1298-1144`

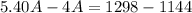
because 4C - 4C =0. This last expression gives

`1.40\text{ A=}154`

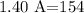
By moving the coefficient of A to the right hand side, we get

`A=(154)/(1.40)`

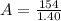
and A is equal to 100, that is A=110.

Now, we can substitute this result into equation (2). It yields

`C+110=286`

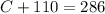
By moving +110 to the right hand side, we have

`C=286-110`

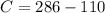
then, C is equal to 176.

Therefore, there are 176 children and 110 adults.