SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the given sides of the first rectangular prism
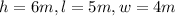
STEP 2: Write the formula for calculating the surface area of the first rectangular prism
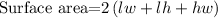
STEP 3: Caclulate the surface area of the first rectangular prism
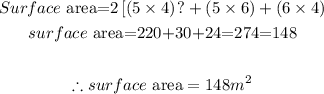
STEP 4: Give the dimensions of a second recatngular prism that will have same surface area
We assume three dimensions that will give same 148 squared meter for the second rectangular prism

Hence, the dimensions of the second rectangular prism that will have the same surface area are:
length = 11m
width = 4m
height = 2m