Given:
The system of equations is
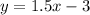
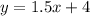
To find:
The true statement about the given system of equations.
Solution:
The slope intercept form of a line is
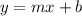
Where, m is the slope and b is the y-intercept.
We have,
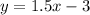
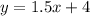
On comparing these two lines with slope intercept form, we get
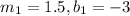
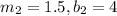
Since the slopes of the lines are equal but the y-intercepts are different, therefore, the two lines are parallel and the system has no solution.
Therefore, the correct option is A.