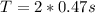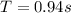Question

The rebounder in basketball has a vertical leap (that is, the vertical movement of a fixed point on their body) of 106 cm .

Answer 1

`u = 4.56m/s`

`T = 0.94s`

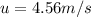
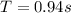
Step-by-step explanation:

See comment for complete question

Given

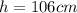`h = 106cm` --- Height

Solving (a): The initial speed

To do this, we make use of the third equation of motion

`v^2=u^2+2ah`

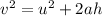
In this case:

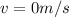`v = 0m/s` --- final velocity at the maximum height

`a = -g = -9.8m/s^2`

`h = 106cm`

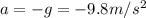
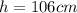
Convert height to metres

`h = 1.06m`

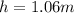
Substitute these values in
`v^2=u^2+2ah`

`0^2 = u^2 +2 *(-9.8) * 1.06`

`0^2 = u^2 -20.776`

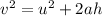
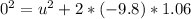
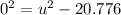
Collect Like Terms

`u^2 =20.776`

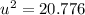
Take the positive square root of both sides

`u =\sqrt{20.776`

`u = 4.55806976691`

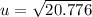
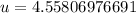
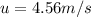`u = 4.56m/s` --- approximated

Hence, the initial velocity is 4.56m/s

Solving (b): Time spent in the air.

This will be solved using the first equation of motion.

`v = u + at`

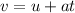
Where:

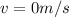`v = 0m/s` --- final velocity at the maximum height

`a = -g = -9.8m/s^2`

`u = 4.56m/s`

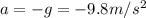
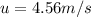
So, we have:

`0 = 4.56 - 9.8t`

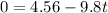
Collect Like Terms

`9.8t = 4.56`

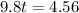
Make t the subject

`t = (4.56)/(9.8)`

`t = 0.46530612244`

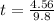
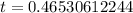
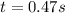`t = 0.47s` --- approximated

The above is the time it reaches the maximum height.

The time it stays in the air is:

`T = 2t`

This gives:

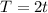
`T = 2*0.47s`

`T = 0.94s`