Answer:
A
Explanation:
We know that to find the area of the rhombus we need the two diagonals. That means that we need the length of
 and
and
 .
.
We can evaluate
 will be 1cm
will be 1cm
 will be 1cm
will be 1cm
Since
 is the midpoint of A to F and
is the midpoint of A to F and
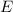 is the midpoint of
is the midpoint of
 (equilateral),
(equilateral),
 is also 1cm.
is also 1cm.
As
 is parallel to
is parallel to
 , we also know that is 1cm.
, we also know that is 1cm.
As
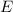 is also the midpoint of
is also the midpoint of
 and
and
 is the midpoint of
is the midpoint of
 ,
,
 must also be 1.
must also be 1.
Since we have one diagonal we can now work out the other using pythagoras' theorem
Let
 be the midpoint of
be the midpoint of

 = √(1^2 - 0.5^2)
= √(1^2 - 0.5^2)
= √(3/4) = √(3)/2
Therefore
 is √(3)/2
is √(3)/2
And
 must then be √3
must then be √3
By using
 and
and
 we can find the area by p*q/2
we can find the area by p*q/2
(√3* 1)/2
Which is A.